I recently saw an argument about how many vertices a cone has. First let me define what a vertex is. A vertex or vertices for plural, is the corner where two points meet. A flat 2D triangle for instance will have 3 vertices, but because a triangle is a 2 dimensional flat shape, it is much easier to determine where its points meet.

How many vertices does a cone have?

When you have a two-dimensional shape like a cone, cube, cylinder, and rectangular prism, determining the amount of vertices becomes more complicated. You have to count the vertices from a three-dimensional angle while also keeping in mind, flat surfaces, make up most 3 D shapes. A cube for instance is just a bunch of 2D Squares joined together. While some have argued that a cone has no vertex because of the rounded meeting point, a cone actually had 1 Vertex as you can see in the picture below. The picture used below is from a popular math text-book used in schools across America.

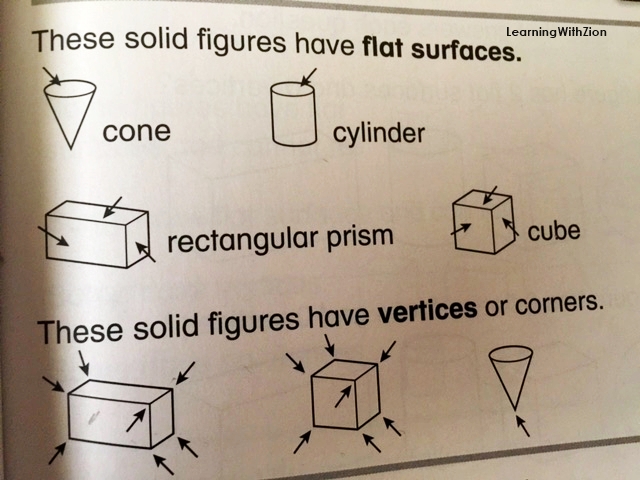
As you can see, even in 2 Dimensional form, a cone has 1 vertex. This does not change in it’s 3D state.

Other 3D Shapes – Flat Surface and Vertices count

As a point of reference the following shapes have the corresponding amount of vertices

A cube had 6 flat surfaces and 8 vertices
A cone has 1 flat surface (the circle at the top) and technically 1 vertex
A rectangular prism has 6 flat surfaces and 8 vertices
A cylinder has 3 flat surfaces and no vertex

The cylinder is the only shape out of those listed we were able to prove categorically that it has no vertex.

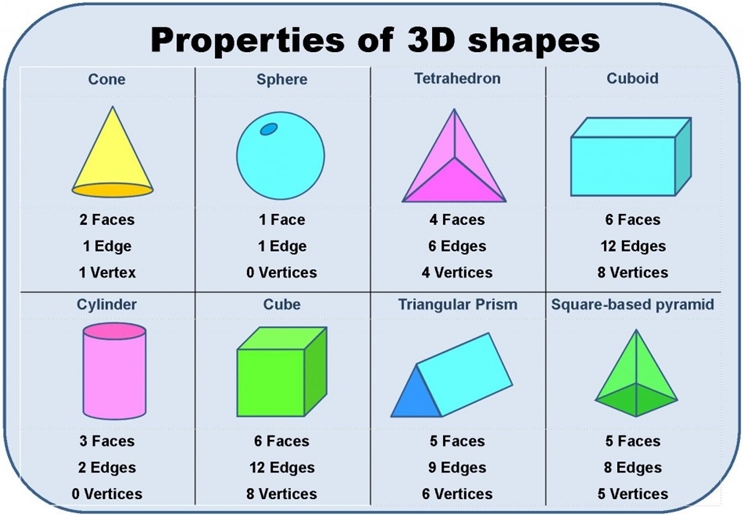
Picture Guide for Shapes and their Vertices

Also, I am sharing a picture guide that depicts the various shapes with the corresponding amount of vertices, faces and edges. You can print or save it for reference use.

I hope this article has been helpful. If you have questions please feel free to comment below.